题目描述
N 件物品和一个容量为 V 的背包,第 i 件物品的重量是 w[i],价值是 v[i],每种物品只有一个,求解将哪些物品装入背包可以使这些物品的总重量和不超过背包容量,且总价值最大。
分析
0-1 背包是最基础的背包问题,其特点为,每种物品只有一个,要么放,要么不放。因此,我们可以将这个问题转化为,对于第 i 个物品,要不要将它放入背包。
令f[i][v] 表示将前 i 件物品放入容量为 v 的背包后获得的最大价值(前 i 件物品未必全都放进了背包)。假设前 i-1 件物品已经被放入背包中,背包容量为 v,此时背包内物品的价值为 f[i-1][v] 。
- 如果选择不放入第 i 件物品,则此时的价值仍为
f[i-1][v]
- 如果选择放入,则此时的价值变为
f[i-1][v-w[i]]+v[i],v-w[i] 表示,为了放入第 i 件物品,前 i-1 件物品所占的空间就只能是 v-w[i]
通过上述分析,就可以得到这样一个状态转移方程f[i][v]=max{f[i-1][v],f[i-1][v-w[i]]+v[i]}
程序-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
#include <iostream>
using namespace std;
int main()
{
int n, v;
cout << "Input item number and backpack volume: ";
cin >> n >> v;
int *w = new int[n+1]();
int *p = new int[n+1]();
cout << "Input item weight and price: " << endl;
for(int i = 1; i <= n; ++i)
{
cin>>w[i]>>p[i];
}
int **f = new int *[n+1]();
for(int i = 0; i <= n; ++i)
{
f[i] = new int[v+1]();
}
for (int i = 0; i <= v; ++i)
{
cout << f[0][i]<< "\t";
}
cout << endl;
for(int i = 1; i <= n; ++i)
{
cout << f[i][0] << "\t";
for (int j = 1; j <= v; ++j)
{
if (j<w[i])
{
f[i][j]=f[i-1][j];
}
else
{
f[i][j] = max(f[i-1][j],f[i-1][j-w[i]]+p[i]);
}
cout << f[i][j] <<"\t";
}
cout << endl;
}
cout << "Result: "<< f[n][v]<<endl;
return 0;
}
|
其结果如下图所示
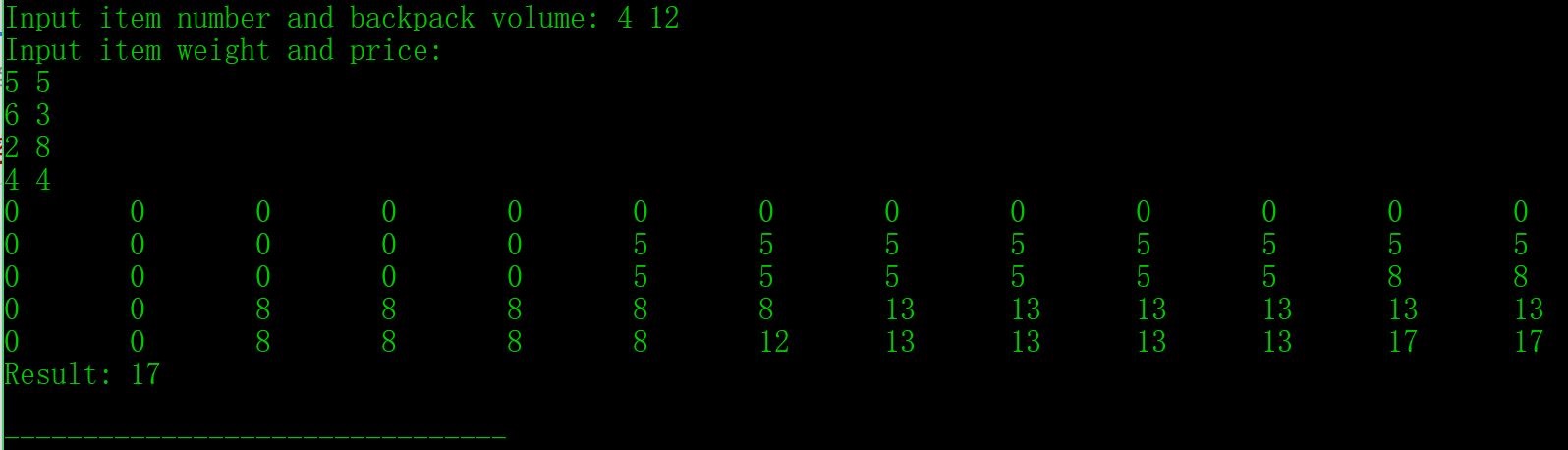
程序-2
上述程序的空间复杂度为 O(n*v),观察前面的递推公式可以发现,f[i][j] 的值仅与 i-1行的值相关,那么,我们就可以不用将整个表格都保存下来,仅保存每一轮循环的计算结果,从而将空间复杂度减少至 O(v)
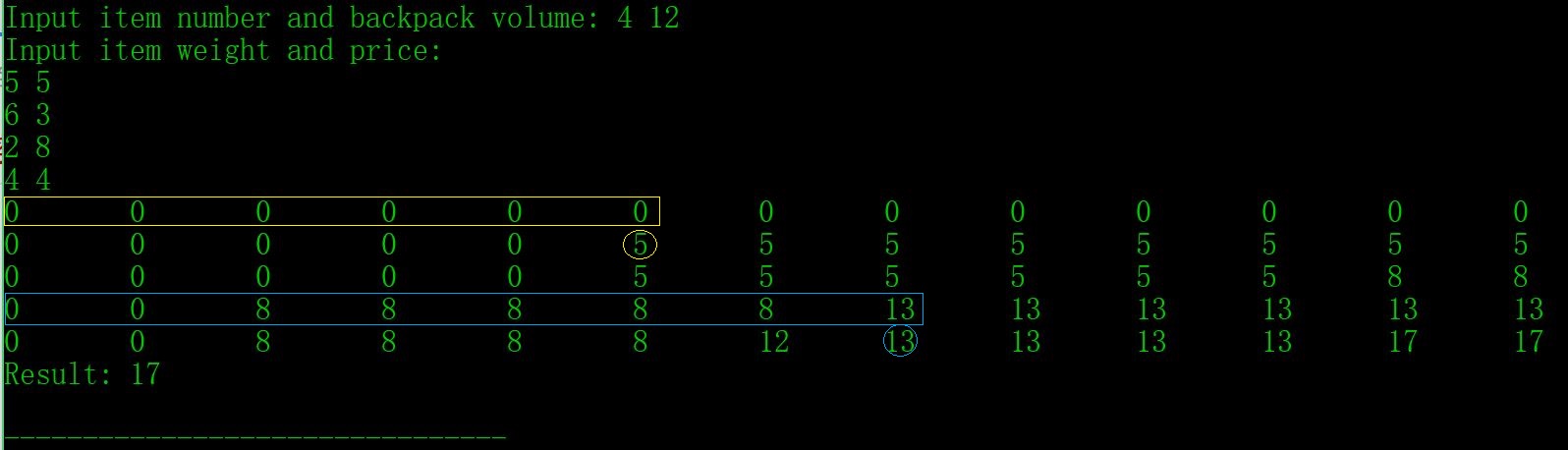
如上图中表格所示,计算黄色圆圈中的元素时,我们所需的数据仅为黄色方框中的数据,而计算蓝色圆圈中的元素时,需要的仅为蓝色方框中的数据。因此,我们可以将 f[i][j] 改为一维数组,且每一次从后向前计算 f 中的元素。修改的程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <iostream>
using namespace std;
int main()
{
int n, v;
cout << "Input item number and backpack volume: ";
cin >> n >> v;
int *w = new int[n+1]();
int *p = new int[n+1]();
cout << "Input item weight and price: " << endl;
for(int i = 1; i <= n; ++i)
{
cin>>w[i]>>p[i];
}
int *f = new int [v+1]();
for (int i = 0; i <=v; ++i)
cout << f[i] << "\t";
cout << endl;
for(int i = 1; i <= n; ++i)
{
for (int j = v; j > 0; --j)
{
if (j >= w[i])
{
f[j] = max(f[j],f[j-w[i]]+p[i]);
}
}
for(int k = 0; k <= v; ++k)
cout << f[k] << "\t";
cout << endl;
}
cout << "Result: "<< f[v]<<endl;
return 0;
}
|
结果如图,与之前程序的结果对比可以发现,输出的 f 是相同的。
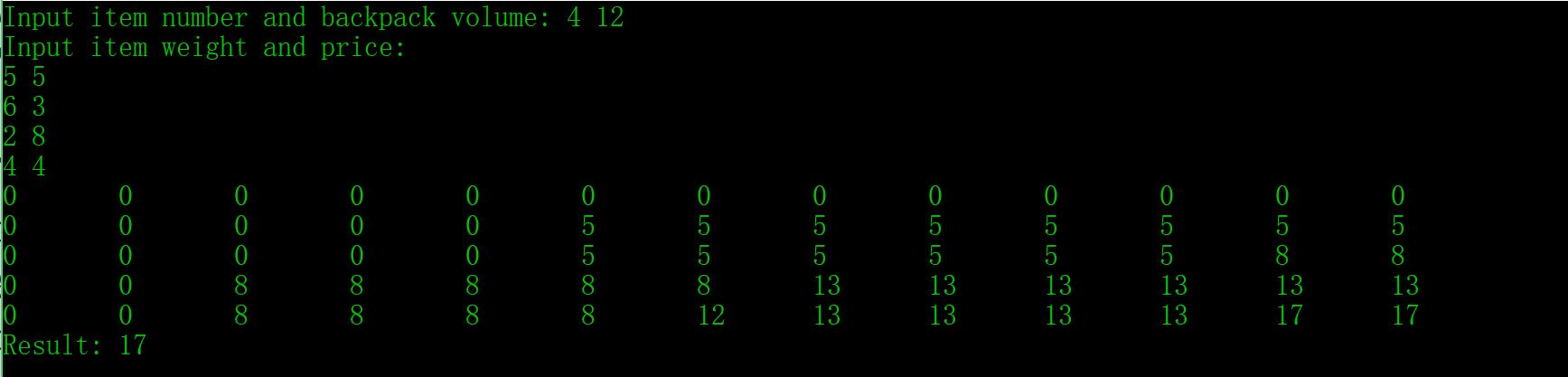
思考
既然最终的结果为数组 f 中的最后一个元素,而改进后的程序每次计算数组f 中的值又是从后向前计算,那么,在最后一轮循环时,我们可以只计算 f 最后的一个值,直接输出结果,而不必再去计算数组中前面部分的值。


